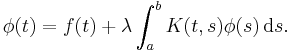Fredholm integral equation
In mathematics, the Fredholm integral equation is an integral equation whose solution gives rise to Fredholm theory, the study of Fredholm kernels and Fredholm operators. The integral equation was studied by Ivar Fredholm.
Contents |
Equation of the first kind
Integral equations, most generally, are common and take many specific forms (Fourier, Laplace, Hankel, etc.). They each differ in their kernels (defined below). What is distinctive about Fredholm integral equations is that they are integral equations in which the integration limits are constants (they do not include the variable). This is contrast to Volterra integral equations.
A homogeneous Fredholm equation of the first kind is written as:
and the problem is, given the continuous kernel function K(t,s), and the function g(t), to find the function f(s).
If the kernel is a function only of the difference of its arguments, namely 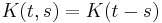 , and the limits of integration are
, and the limits of integration are 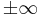 , then the right hand side of the equation can be rewritten as a convolution of the functions K and f and therefore the solution will be given by
, then the right hand side of the equation can be rewritten as a convolution of the functions K and f and therefore the solution will be given by
where  and
and 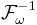 are the direct and inverse Fourier transforms respectively.
are the direct and inverse Fourier transforms respectively.
Equation of the second kind
An inhomogeneous Fredholm equation of the second kind is given as
Given the kernel K(t,s), and the function 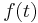 , the problem is typically to find the function
, the problem is typically to find the function 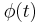 . A standard approach to solving this is to use the resolvent formalism; written as a series, the solution is known as the Liouville-Neumann series.
. A standard approach to solving this is to use the resolvent formalism; written as a series, the solution is known as the Liouville-Neumann series.
General theory
The general theory underlying the Fredholm equations is known as Fredholm theory. One of the principal results is that the kernel K is a compact operator, known as the Fredholm operator. Compactness may be shown by invoking equicontinuity. As an operator, it has a spectral theory that can be understood in terms of a discrete spectrum of eigenvalues that tend to 0.
Applications
Fredholm equations arise naturally in the theory of signal processing, most notably as the famous spectral concentration problem popularized by David Slepian. They also commonly arise in linear forward modeling and inverse problems.
See also
References
- Integral Equations at EqWorld: The World of Mathematical Equations.
- A.D. Polyanin and A.V. Manzhirov, Handbook of Integral Equations, CRC Press, Boca Raton, 1998. ISBN 0-8493-2876-4
- Khvedelidze, B.V.; Litvinov, G.L. (2001), "Fredholm kernel", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=F/f041440
- F. J. Simons, M. A. Wieczorek and F. A. Dahlen. Spatiospectral concentration on a sphere. SIAM Review, 2006, doi:10.1137/S0036144504445765
- D. Slepian, "Some comments on Fourier Analysis, uncertainty and modeling", SIAM Review, 1983, Vol. 25, No. 3, 379-393.
- Salam, Nishan-e-Imtiaz, Abdus; Matthews, Paul T. (1966). "§Integral Equations". Selected Papers of Abdus Salam (1st ed.). Washington D.C.: World Scientific Publications. ISBN 981-0-216-6629. http://books.google.com/books?id=Bw4FUKdDbaUC&pg=PA391&lpg=PA391&dq=ABdus+Salam%27s+field+equations+d&source=bl&ots=NnAfG69OOH&sig=K70sVXiSO56P_3sHHrYR9fTrp4w&hl=en&ei=K3NgTr2FFaXXiALI0NWoDg&sa=X&oi=book_result&ct=result&resnum=1&ved=0CBYQ6AEwAA#v=onepage&q&f=false.
- Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007). "Section 19.1. Fredholm Equations of the Second Kind". Numerical Recipes: The Art of Scientific Computing (3rd ed.). New York: Cambridge University Press. ISBN 978-0-521-88068-8. http://apps.nrbook.com/empanel/index.html#pg=989.
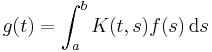
\over
\mathcal{F}_t[K(t)](\omega)}
\right]=\int_{-\infty}^\infty {\mathcal{F}_t[g(t)](\omega)\over
\mathcal{F}_t[K(t)](\omega)}e^{2\pi i \omega t} \mathrm{d}\omega](/2012-wikipedia_en_all_nopic_01_2012/I/c9ebeab45e416eff69e8774cb909856e.png)